Thomas Whitehead

Thomas Whitehead
Member of Jesus College
PhD student in Dr Conduit's group
Office: 546 Mott Bld
Phone: +44(0)1223 3 37467
Email: tmw38 @ cam.ac.uk
Personal web site
TCM Group, Cavendish Laboratory
19 JJ Thomson Avenue,
Cambridge, CB3 0HE UK.
Research
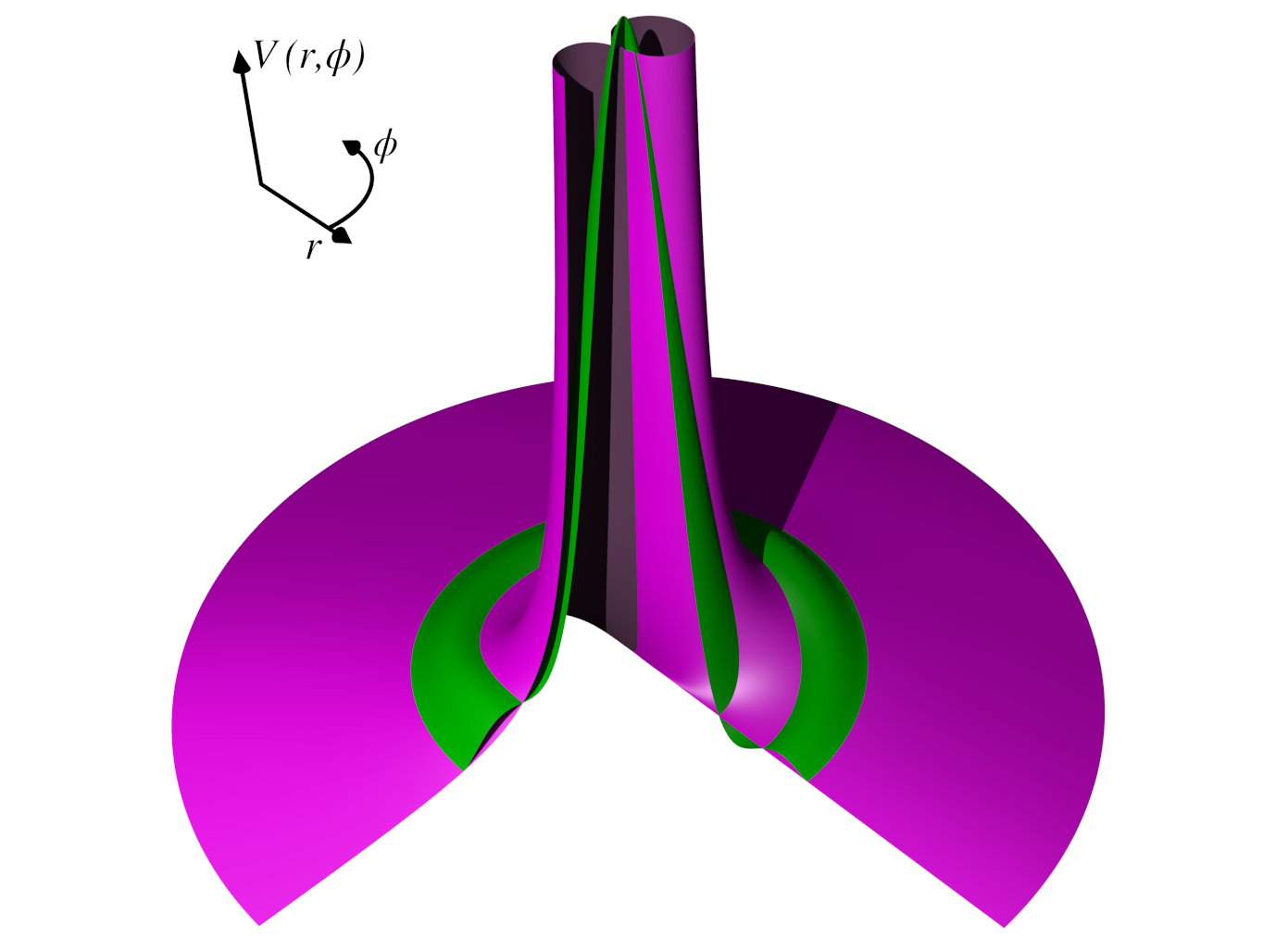
I am interested in the way large systems of electrons or other particles can interact to give rise to phenomena not present in small or non-interacting systems. A particularly interesting problem is found when considering the interaction of particles with dipole moments. The dipolar interaction is divergent at particle coalescence, which makes the use of numerical techniques to investigate systems interacting via the dipolar potential inefficient. To get around this problem we construct pseudopotentials that capture the correct physics of the dipolar system, but are finite and smooth at particle coalescence, and hence easier to work with numerically. These can give a speed-up of over 2000 times when compared to using the real dipolar interaction. An example pseudopotential for the dipolar interaction is shown in green, with the real (and divergent) dipolar potential in magenta.
We test these new pseudopotentials in two-body and many-body simulations, where they have accuracies of around 0.001% and 0.01% respectively, which allows them to be used in place of the real dipolar interaction in studies of systems of dipolar particles. One particularly attractive system to study is a two-dimensional gas of quantum-degenerate fermionic dipolar particles (experimentally these could be molecules with an electric dipole moment [Park et al., Phys. Rev. Lett. 114, 205302 (2015)]), where all the dipole moments are aligned either normal to or at an angle to their plane of motion. It has been predicted that this system should have a rich phase diagram, which the use of pseudopotentials will allow us to explore with the use of quantum Monte Carlo simulations using the casino code.

In Plain English
Systems made up of large numbers of particles often behave in interesting and unexpected ways. For example, the strength of the interactions between the particles can mean that the system could change between being a gas or a crystal at low temperatures. The best way to find out what will happen is often to run computer simulations of the system: but this can take a long time if the interactions between particles are not well-behaved. This is the subject of my current research: to make a 'pretend' interaction that accurately captures the physics of the dipolar interaction, but isn't as spiky and computationally intensive.
Featured Publications
Publications
Multipa
rticle instability in a spin-imbalanced Fermi gas, Physical Review B 97, 014502 (2018).
Also available at arXiv:1712.09847 and as a pdf (© APS).
Jastrow correlation factor for periodic systems, Physical Review B 94, 035157 (2016).
Also available at arXiv:1607.05921 and as a pdf (© APS).
Pseudopotential for the two-dimensional contact interaction, Physical Review A 93, 042702 (2016).
Also available at arXiv:1603.05001 and as a pdf (© APS).
Pseudopotentials for an ultracold dipolar gas, Physical Review A 93, 022706 (2016).
Also available at arXiv:1601.07746 and as a pdf (© APS).
Parametrizing unresolved mesoscale motions in NAME, Met Office Forecasting Research Technical Report, May 2015.
Presentations
A multi-particle superconductor?, Cavendish Graduate Student Conference, University of Cambridge, 1 December 2016; and Frontiers of Condensed Matter Physics, University of Bristol, 10 January 2017.
The ν Jastrow factor, Electronic Structure Discussion Group, TCM, University of Cambridge, 9 March 2016.
Pseudopotentials for a dipolar ultracold atomic gas, Electronic Structure Discussion Group, TCM, University of Cambridge, 18 March 2015; and Quantum Cambridge Winter School, St Hugh's College Oxford, 20-23 March 2015.
Posters
Pseudopotentials for an ultracold dipolar gas, New States of Matter and their Excitations, Helmholtz Virtual Institute, 18 June 2015; Physics by the Lake, Cumberland Lodge, 2-15 August 2015; Jesus College Graduate Student Conference, 12 March 2016; and Long-Range Interacting Many-Body Systems: from Atomic to Astrophysical Scales, ICTP, Trieste, 25-29 July 2016.