Joseph Prentice

Dr Joseph Prentice
Member of St Edmund's College
Visitor in Prof Needs' group
Office: 517 Mott Bld
Phone: +44(0)1223 7 64164
Email: jcap3 @ cam.ac.uk
Personal web site
TCM Group, Cavendish Laboratory
19 JJ Thomson Avenue,
Cambridge, CB3 0HE UK.
Research
I am interested in modelling and computing properties of solid state systems from first principles, using, among other methods, DFT as implemented in CASTEP. Specifically, I investigate anharmonic vibrational effects in such materials, using the vibrational self-consistent field (VSCF) method of Monserrat, Drummond and Needs (2013)
I am currently interested in calculating the anharmonic properties of dynamic Jahn-Teller systems, in order to describe the Jahn-Teller effect in such systems correctly. The dynamic Jahn-Teller effect is fundamentally an anharmonic one, so a method that includes anharmonicity, such as VSCF, is required if it is to emerge from first principles calculations. In particular, our method allows us to calculate the anharmonic vibrational wavefunction, which can directly show the presence of a dynamic Jahn-Teller effect. I am studying several dynamic Jahn-Teller systems, including defects and materials at high temperatures and pressures. I am also interested in making improvements to the VSCF method by reducing the computational cost and including coupling between phonons, increasing the accuracy of the method.
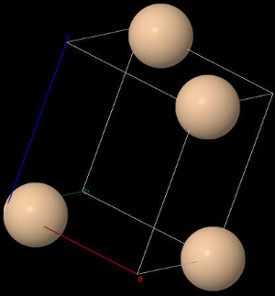
The picture shows an example of a tetragonal distortion around a vacancy in the diamond structure, where the 4 nearest neighbours form two pairs. This structure is the static Jahn-Teller distortion which appears in silicon, but does not appear in diamond due to the dynamic Jahn-Teller effect keeping the structure tetrahedral.

In Plain English
In many solid materials, the atoms that make up the material organise themselves into a repeating crystal structure. In some situations, however, the atoms can lower the overall energy of the system by distorting away from the perfect crystal structure. This can happen if there is a flaw in the crystal structure (a defects), such as a missing atom (a vacancy), or just due to the more regular structure being unstable - perhaps because two atoms are too close together, or too far apart. When a system distorts itself away from a high symmetry structure to a lower symmetry one, this is known as a static Jahn-Teller effect.
However, if we include the fact that the atoms are also vibrating around their equilibrium positions, the energy can change significantly, depending on how light the nuclei are (lighter ones will vibrate more strongly) and the temperature of the system (higher temperatures mean larger vibrations). In some cases, the effect of this can be to overrule the static Jahn-Teller effect and prevent the system from distorting itself so much. This is called the dynamic Jahn-Teller effect. In rough terms, the atoms vibrate so much that they are able to `hop' randomly between equivalent distortions - for example, if the system can equally well have a static Jahn-Teller distortion in the x,y and z directions, in a dynamic Jahn-Teller distortion the system `hops' between them. This gives an average distortion of zero, essentially putting the system back into the higher symmetry structure again!
Dynamic Jahn-Teller systems can be extremely technologically important, for example the neutral vacancy and Si-V defect in diamond. This makes it important to understand their properties and how they behave. My work aims to provide a thorough theoretical understanding of these defects by predicting their behavior using first principles calculations, and comparing to known results.
I also work to improve the methods by which we calculate the effect of these vibrations, making them less time consuming and costly, as well as improving their accuracy significantly. This will allow more complex systems to be studied.
Featured Publications
- Using forces to accelerate first-principles anharmonic vibrational calculations Phys. Rev. Materials 1 023801 (2017)
- First-principles study of the dynamic Jahn-Teller distortion of the neutral vacancy in diamond Phys. Rev. B 95 014108 (2017)
- Modeling the angle-dependent magnetoresistance oscillations of Fermi surfaces with hexagonal symmetry Phys. Rev. B 93 245105 (2016)